Lingkaran

Loncat ke navigasi Loncat ke pencarian

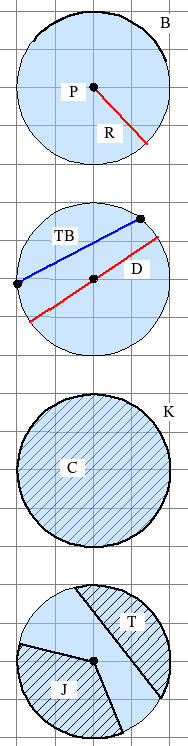
Elemen-elemen suatu lingkaran.

Dalam geometri Euklid, sebuah lingkaran adalah himpunan semua titik pada bidang dalam jarak tertentu, yang disebut jari-jari, dari suatu titik tertentu, yang disebut pusat. Lingkaran adalah contoh dari kurva tertutup sederhana, membagi bidang menjadi bagian dalam dan bagian luar.

Daftar isi

• 1 Istilah dalam lingkaran
• 2 Persamaan
  • 2.1 Persamaan parametrik
• 3 Luas lingkaran
  • 3.1 Penjumlahan elemen juring
  • 3.2 Luas juring
  • 3.3 Luas tembereng
  • 3.4 Luas cincin lingkaran
  • 3.5 Luas potongan cincin lingkaran
• 4 Keliling lingkaran
  • 4.1 Panjang busur lingkaran
• 5 π (Pi)
• 6 Referensi
• 7 Pustaka
• 8 Pranala luar

Istilah dalam lingkaran

Beberapa istilah geometri mengenai lingkaran, yaitu:

• Istilah yang menunjukkan titik, yaitu:
  1. Titik pusat (P)
     merupakan titik tengah lingkaran, di mana jarak titik tersebut dengan titik manapun pada lingkaran selalu tetap.
• Istilah yang menunjukkan garisan, yaitu:
  1. Jari-jari (R)
     merupakan garis lurus yang menghubungkan titik pusat dengan lingkaran.
  2. Tali busur (TB)
     merupakan garis lurus di dalam lingkaran yang memotong lingkaran pada dua titik yang berbeda.
  3. Busur (B)
     merupakan garis lengkung baik terbuka, maupun tertutup yang berimpit dengan lingkaran.
  4. Keliling lingkaran (K)
     merupakan busur terpanjang pada lingkaran.
  5. Diameter (D)
     merupakan tali busur terbesar yang panjangnya adalah dua kali dari jari-jarinya. Diameter ini membagi lingkaran sama luas.
  6. Apotema
     merupakan garis terpendek antara tali busur dan pusat lingkaran.
• Istilah yang menunjukkan luasan, yaitu:
  1. Juring (J)
     merupakan daerah pada lingkaran yang dibatasi oleh busur dan dua buah jari-jari yang berada pada kedua ujungnya.
  2. Tembereng (T)
     merupakan daerah pada lingkaran yang dibatasi oleh sebuah busur dengan tali busurnya.
  3. Cakram (C)
     merupakan semua daerah yang berada di dalam lingkaran. Luasnya yaitu jari-jari kuadrat dikalikan dengan pi. Cakram merupakan juring terbesar.

Persamaan

Suatu lingkaran memiliki persamaan

${\displaystyle (x-x_{0})^{2}+(y-y_{0})^{2}=R^{2}\!}$

dengan ${\displaystyle R\!}$ adalah jari-jari lingkaran dan ${\displaystyle (x_{0},y_{0})\!}$ adalah koordinat pusat lingkaran.
Jika pusat lingkaran terdapat di ${\displaystyle (0,0)\!}$, maka persamaan di atas dapat dituliskan sebagai

${\displaystyle x^{2}+y^{2}=R^{2}\!}$

Bentuk persamaan lingkaran dapat dijabarkan juga menjadi bentuk

${\displaystyle x^{2}+Ax+y^{2}+By+C=0\!}$

dengan ${\displaystyle {\sqrt {{\frac {A^{2}+B^{2}}{4}}-C}}\!}$ adalah jari-jari lingkaran dan ${\displaystyle (-{\frac {A}{2}},-{\frac {B}{2}})\!}$ adalah koordinat pusat lingkaran. Bentuk persamaan tersebut dikenal sebagai bentuk umum persamaan lingkaran.

Persamaan parametrik

Lingkaran dapat pula dirumuskan dalam suatu persamaan parameterik, yaitu

${\displaystyle x=x_{0}+R\cos(t)\!}$

${\displaystyle y=y_{0}+R\sin(t)\!}$

yang apabila dibiarkan menjalani t akan dibuat suatu lintasan berbentuk lingkaran dalam ruang x-y.

Luas lingkaran

Luas lingkaran

Luas lingkaran memiliki rumus

${\displaystyle A=\pi R^{2}\!}$

yang dapat diturunkan dengan melakukan integrasi elemen luas suatu lingkaran

${\displaystyle dA=rd\theta \ dr}$

dalam koordinat polar, yaitu

${\displaystyle \int dA=\int _{r=0}^{R}\int _{\theta =0}^{2\pi }rd\theta \ dr=\int _{r=0}^{R}rdr\int _{\theta =0}^{2\pi }d\theta ={\frac {1}{2}}(R^{2}-0^{2})\ (2\pi -0)=\pi R^{2}\!}$

Dengan cara yang sama dapat pula dihitung luas setengah lingkaran, seperempat lingkaran, dan bagian-bagian lingkaran. Juga tidak ketinggalan dapat dihitung luas suatu cincin lingkaran dengan jari-jari dalam ${\displaystyle R_{1}\!}$ dan jari-jari luar ${\displaystyle R_{2}\!}$.

Penjumlahan elemen juring

Luas lingkaran dapat dihitung dengan memotong-motongnya sebagai elemen-elemen dari suatu juring untuk kemudian disusun ulang menjadi sebuah persegi panjang yang luasnya dapat dengan mudah dihitung. Dalam gambar r berarti sama dengan R yaitu jari-jari lingkaran.

Luas juring

Luas juring suatu lingkaran dapat dihitung apabila luas lingkaran dijadikan fungsi dari R dan θ, yaitu;

${\displaystyle A(R,\theta )={\frac {1}{2}}R^{2}\theta \!}$

dengan batasan nilai θ adalah antara 0 dan 2π. Saat θ bernilai 2π, juring yang dihitung adalah juring terluas, atau luas lingkaran.
Luas juring adalah ${\displaystyle {\frac {\theta }{360}}\pi r^{2}}$ atau ${\displaystyle {\frac {\theta }{2}}r^{2}}$

Luas tembereng

Luas tembereng = Luas juring - Luas segitiga sama kaki.

Luas cincin lingkaran

Suatu cincin lingkaran memiliki luas yang bergantung pada jari-jari dalam ${\displaystyle r}$ dan jari-jari luar ${\displaystyle R}$, yaitu

${\displaystyle A_{cincin}=\pi (R^{2}-r^{2})\!}$

di mana untuk ${\displaystyle r=0\!}$ rumus ini kembali menjadi rumus luas lingkaran.

Luas potongan cincin lingkaran

Dengan menggabungkan kedua rumus sebelumnya, dapat diperoleh

${\displaystyle A_{potongan\ cincin}={\frac {\pi }{2}}(R^{2}-r^{2})\theta \!}$

yang merupakan luas sebuah cincin tak utuh.

Keliling lingkaran

Keliling lingkaran memiliki rumus:

${\displaystyle K=2\pi R\!}$

Panjang busur lingkaran

Panjang busur suatu lingkaran dapat dihitung dengan menggunakan rumus

${\displaystyle L=R\theta \!}$

yang diturunkan dari rumus untuk menghitung panjang suatu kurva

${\displaystyle dL=\int {\sqrt {1+\left({\frac {dy}{dx}}\right)^{2}}}dx\!}$

di mana digunakan

${\displaystyle y=\pm {\sqrt {R^{2}-x^{2}}}\!}$

sebagai kurva yang membentuk lingkaran. Tanda ${\displaystyle \pm }$ mengisyaratkan bahwa terdapat dua buah kurva, yaitu bagian atas dan bagian bawah. Keduanya identik (ingat definisi lingkaran), sehingga sebenarnya hanya perlu dihitung sekali dan hasilnya dikalikan dua.
Panjang busur adalah ${\displaystyle {\frac {\theta }{360}}2\pi r}$ atau r


 Sumber: https://id.wikipedia.org/wiki/Lingkaran

 ${\displaystyle \theta r}$